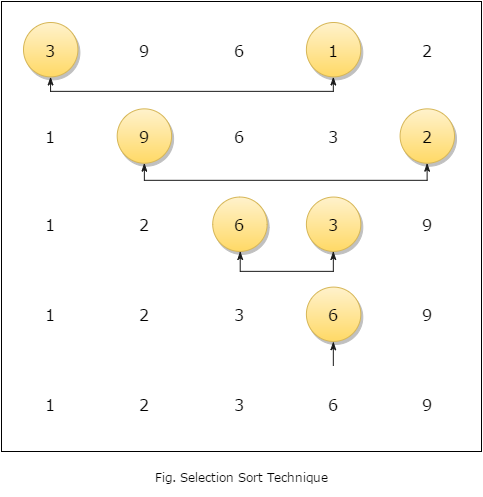
Selection sort
Selection sort is a simple sorting algorithm. In this sort, the array is divided into two parts as the unsolved part at the right and the solved part at the left. In this method, the 0th element(first element) is compared with all the other elements in the array to check whether it’s the minimum value. If the value of the 0th element is greater than the compared value, the position of the 2 elements will be interchanged. In this way after the first iteration, the element with the smallest value is placed in the 0th position(1st position). This process will be repeated until the full array gets sorted. This method can be used to sort arrays in both ascending and descending order.
Pyramids and patterns
This example will help you in creating the following patterns using go language as below.


Palindrome
This program will help you to identify whether an input number or string is a palindrome or not. A string is identified as a palindrome if the reverse of the string is also the same as the original string. This is the same for numbers as well.
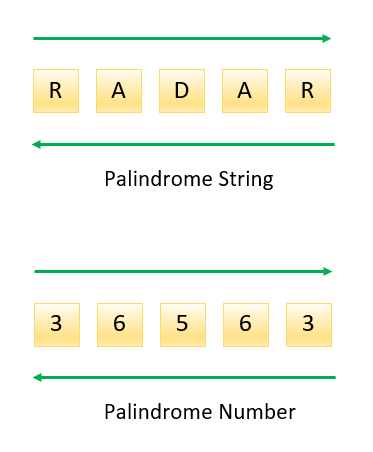
Here, the first function (palindromeNumber()) is checking whether the number is a palindrome or not. The second function (palindromeString(word)) is checking whether the input string is a palindrome or not.
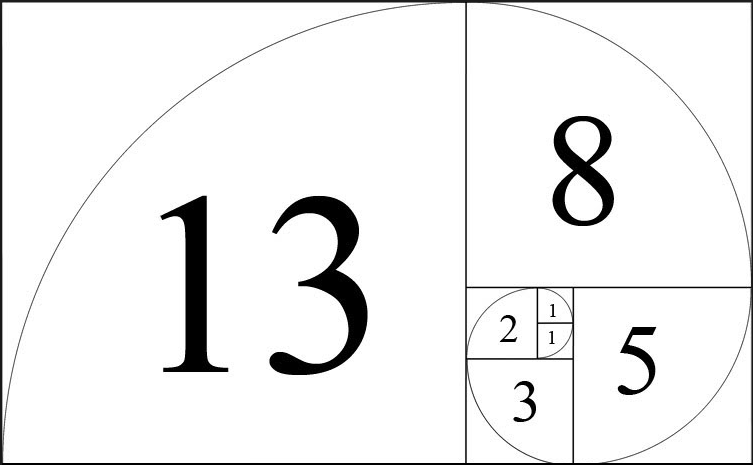
Fibonacci Sequence
Fibonacci numbers are the numbers which follow the sequence given below.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ……..
The sequence of Fn of Fibonacci numbers is defined by the recurrence relation.
Fn = Fn-1 + Fn-2
When we make squares with the following widths (0, 1, 1, 2, 3, 5, 8,.........) it makes a nice spiral.
Bubble Sort
Bubble sort is the simplest of all the sorting algorithms and its used to sort a given set of elements in the form of an array. It works by stepping through the array repeatedly, swapping the adjacent elements if they are not in order. Bubble sort compares all the elements one by one and arranges the elements in the ascending order based on their values.
First Pass:
( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1.
( 1 5 4 2 8 ) –> ( 1 4 5 2 8 ), Swap since 5 > 4
( 1 4 5 2 8 ) –> ( 1 4 2 5 8 ), Swap since 5 > 2
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
Second Pass:
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )
( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), Swap since 4 > 2
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
Third Pass:
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )